The nature of magnetic dipoles.
a. A “Gilbert” dipole consists of a pair of magnetic monopoles each with a magnitude q_{m} but opposite magnetic charges separated by a distance d, where d is small. In this case, assume that -q_{m} is located at z=0 and +q_{m} is located at z=d.

Assume that magnetic monopoles behave like electric monopoles according to a coulomb-like force
and the magnetic field obeys
i. What are the dimensions of the quantity q_{m} ?
ii. Write an exact expression for the magnetic field strength B(z) along the z axis as a function of z for z>d. Write your answer in terms of q_{m}, d, z, and any necessary fundamental constants.
iii. Evaluate this expression in the limit as d \rightarrow 0, assuming that the product q_{m} d=p_{m} is kept constant, keeping only the lowest non-zero term. Write your answer in terms of p_{m}, z, and any necessary fundamental constants.
b. An “Ampère” dipole is a magnetic dipole produced by a current loop I around a circle of radius r, where r is small. Assume the that the z axis is the axis of rotational symmetry for the circular loop, and the loop lies in the x y plane at z=0.
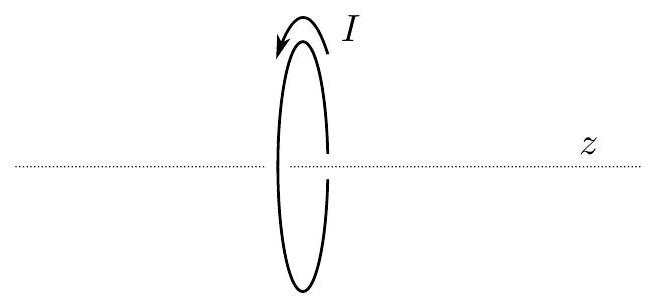
i. Write an exact expression for the magnetic field strength B(z) along the z axis as a function of z for z>0. Write your answer in terms of I, r, z, and any necessary fundamental constants.
ii. Let k I r^{\gamma} have dimensions equal to that of the quantity p_{m} defined above in Part aiii, where k and \gamma are dimensionless constants. Determine the value of \gamma.
iii. Evaluate the expression in Part bi in the limit as r \rightarrow 0, assuming that the product k I r^{\gamma}=p_{m}^{\prime} is kept constant, keeping only the lowest non-zero term. Write your answer in terms of k, p_{m}^{\prime}, z, and any necessary fundamental constants.
iv. Assuming that the two approaches are equivalent, p_{m}=p_{m}^{\prime}. Determine the constant k in Part bii.
c. Now we try to compare the two approaches if we model a physical magnet as being composed of densely packed microscopic dipoles.
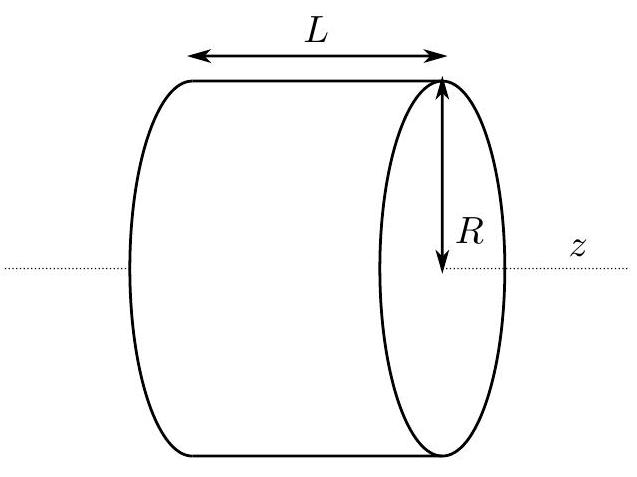
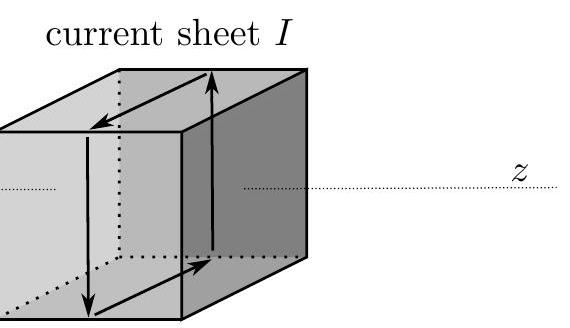
A cylinder of this uniform magnetic material has a radius R and a length L. It is composed of N magnetic dipoles that could be either all Ampère type or all Gilbert type. N is a very large number. The axis of rotation of the cylinder and all of the dipoles are all aligned with the z axis and all point in the same direction as defined above so that the magnetic field outside the cylinder is the same in either dipole case as you previously determined. Below is a picture of the two dipole models; they are cubes of side d \ll<R and d \ll L with volume v_{m}=d^{3}.
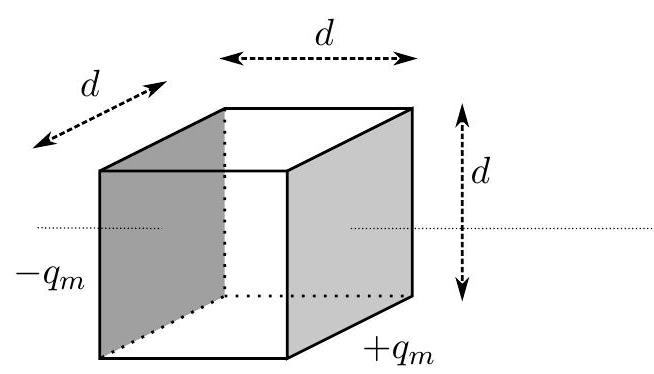
i. Assume that R \gg L and only Gilbert type dipoles, determine the magnitude and direction of B at the center of the cylinder in terms of any or all of p_{m}, R, L, v_{m}, and any necessary fundamental constants.
ii. Assume that R \ll L and only Ampère type dipoles, determine the magnitude and direction of B at the center of the cylinder in terms of any or all of p_{m}, R, L, v_{m}, and any necessary fundamental constants.