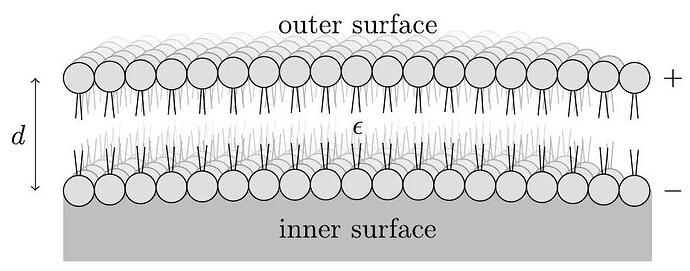
The wall of a neuron is made from an elastic membrane, which resists compression in the same way as a spring. It has an effective spring constant k and an equilibrium thickness d_{0}. Assume that the membrane has a very large area A and negligible curvature.
The neuron has “ion pumps” that can move ions across the membrane. In the resulting charged state, positive and negative ionic charge is arranged uniformly along the outer and inner surfaces of the membrane, respectively. The permittivity of the membrane is \epsilon.
a. Suppose that, after some amount of work is done by the ion pumps, the charges on the outer and inner surfaces are Q and -Q, respectively. What is the thickness d of the membrane?
b. Derive an expression for the voltage difference V between the outer and inner surfaces of the membrane in terms of Q and the other parameters given.
c. Suppose that the ion pumps are first turned on in the uncharged state, and the membrane is charged very slowly (quasistatically). The pumps will only turn off when the voltage difference across the membrane becomes larger than a particular value V_{\text {th }}. How large must the spring constant k be so that the ion pumps turn off before the membrane collapses?
d. How much work is done by the ion pumps in each of the following situations? Express your answers in terms of k and d_{0}.
i. k is infinitesimally larger than the value derived in part (c).
ii. k is infinitesimally smaller than the value derived in part (c).
Assume in each case that the membrane thickness d cannot become negative.