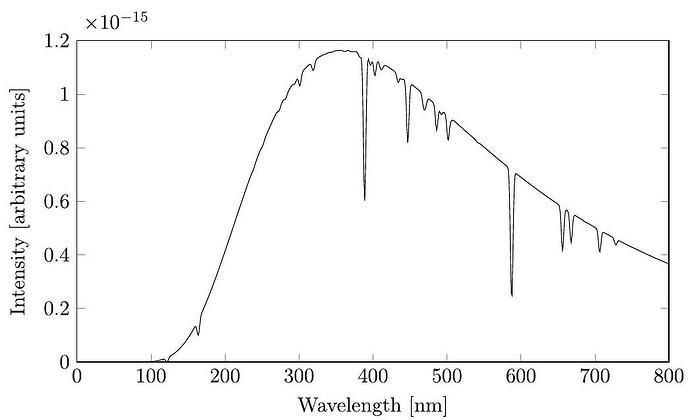
Scientists have recently detected a new star, the MAR-Kappa. The star is almost a perfect blackbody, and its measured light spectrum is shown below.
The total measured light intensity from MAR-Kappa is I=1.12 \times 10^{-8} \mathrm{~W} / \mathrm{m}^{2}. The mass of MAR-Kappa is estimated to be 3.5 \times 10^{30} \mathrm{~kg}. It is stationary relative to the sun. You may find the Stefan-Boltzmann law useful, which states the power emitted by a blackbody with area A is \sigma A T^{4}.
a. The spectrum of wavelengths \lambda emitted from a blackbody only depends on h, c, k_{B}, \lambda, and T. Given that the sun has a surface temperature of 5778 \mathrm{~K} and peak emission at 500 \mathrm{~nm}, what is the approximate surface temperature of MAR-Kappa?
b. The “lines” in the spectrum result from atoms in the star absorbing specific wavelengths of the emitted light. One contribution to the width of the spectral lines is the Doppler shift associated with the thermal motion of the atoms in the star. The spectral line at \lambda=389 \mathrm{~nm} is due to helium. Estimate to within an order of magnitude the thermal broadening \Delta \lambda of this line. The mass of a helium atom is 6.65 \times 10^{-27} \mathrm{~kg}.
c. Over the course of a year, MAR-Kappa appears to oscillate between two positions in the background night sky, which are an angular distance of 1.6 \times 10^{-6} \mathrm{rad} apart. How far away is MAR-Kappa? Assume that MAR-Kappa lies in the same plane as the Earth’s orbit, which is circular with radius 1.5 \times 10^{11} \mathrm{~m}.
d. What is the radius of MAR-Kappa?
Over the course of some time, you observe that the star’s intensity periodically dips from I to \left(1-10^{-5}\right) I and then rises back to I, with period t. One possible explanation for this observation is that an exoplanet is orbiting the star and blocking the starlight for some time.
e. Estimate the exoplanet’s radius, assuming that it is much closer to the star than to the Earth.
f. Assume the exoplanet is a blackbody with uniform temperature in a circular orbit around the star. What must t be so that the planet has a temperature of 250 \mathrm{~K} ? (If this were true, and the planet had an appropriate atmosphere, the temperature would increase enough to support life.)