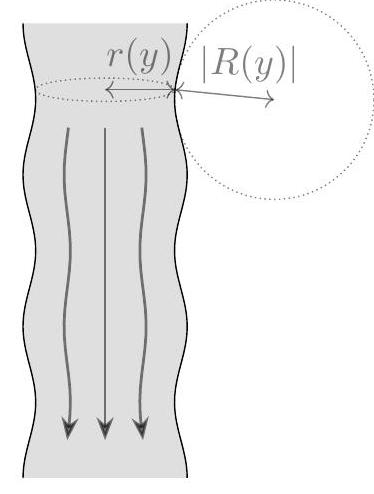
a. When a faucet is turned on, a stream of water flows down with initial speed v_{0} at the spout. For this problem, we define y to be the vertical coordinate with its positive direction pointing up.
Assuming the water speed is only affected by gravity as the water falls, find the speed of water v(y) at height y. Define the zero of y such that the equation for v^{2} has only one term and find y_{0}, the height of the spout.
b. Assume that the stream of water falling from the faucet is cylindrically symmetric about a vertical axis through the center of the stream. Also assume that the volume of water per unit time exiting the spout is constant, and that the shape of the stream of water is constant over time.
In this case, the radius r of the stream of water is a function of vertical position y. Let the radius at the faucet be r_{0}. Using your result from part (a), find r(y).
If r(y) is not constant, it implies that the water has some radial velocity during its fall, in contradiction to our assumptions in part (a) that the motion is purely vertical. You may assume throughout the problem that any such radial velocity is negligibly small.
c. The water-air interface has some surface tension, \sigma. The effect of surface tension is to change the pressure in the stream according to the Young-Laplace equation,
where \Delta P is the difference in pressure between the stream and the atmosphere and R is the radius of curvature of the vertical profile of the stream, visualized below. ( R<0 for the stream of water; the radius of curvature would be positive only if the stream profile curved inwards.)
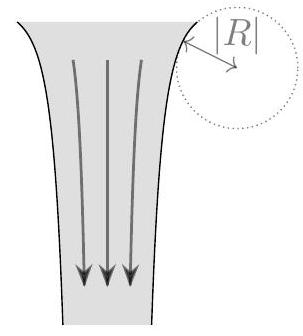
For this part of the problem, we assume that |R| \gg|r|, so that the curvature of the vertical profile of the stream can be ignored. Also assume that water is incompressible.
Accounting for the pressure in the stream, find a new equation relating for r(y) in terms of \sigma, r_{0}, v_{0}, and \rho, the density of water. You do not need to solve the equation for r.
d. After falling for some distance, the water stream usually breaks into smaller droplets. This occurs because small random perturbations to the shape of the stream grow over time, eventually breaking the stream into apart.
For the rest of this problem we ignore the change in the radius of the stream due to changing speed of the water, as considered earlier. Instead, we examine small random variations in the radius of the stream.
Random variations can be broken down into a sum of sinusoidal variations in stream radius, each with a different wavenumber k. We can analyze these different sinusoidal variations independently.
Consider a stream of water whose radius obeys
where A \ll r_{0} is the perturbation amplitude. To analyze such a stream, it is sufficient to consider only the thickest and thinnest parts of the stream.
Accounting for both sources of curvature, find a condition on r_{0} and k such that the size of perturbations increases with time.