A disk of uniform mass density, mass M, and radius R sits at rest on a frictionless floor. The disk is attached to the floor by a frictionless pivot at its center, which keeps the center of the disk in place, but allows the disk to rotate freely. An ant of mass m \ll M is initially standing on the edge of the disk; you may give your answers to leading order in m / M.
a. The ant walks an angular displacement \theta along the edge of the disk. Then it walks radially inward by a distance h \ll R, tangentially through an angular displacement -\theta, then back to its starting point on the disk. Assume the ant walks with constant speed v.
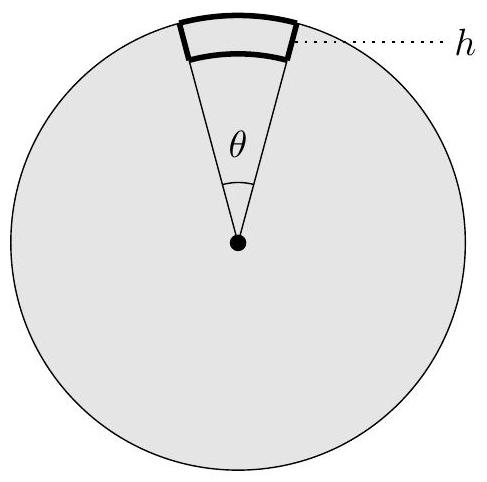
Through what net angle does the disk rotate throughout this process, to leading order in h / R ?
b. Now suppose the ant walks with speed v along a circle of radius r, tangent to its starting point.
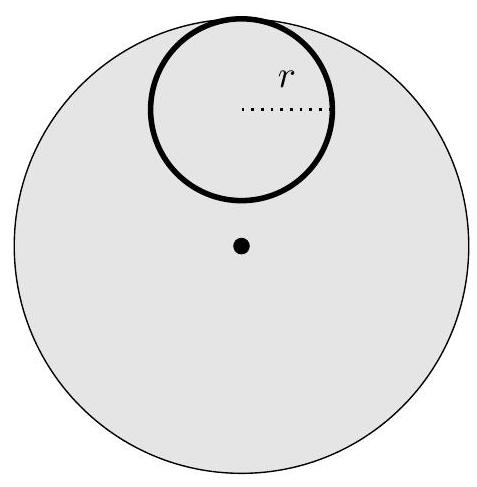
Through what net angle does the disk rotate?